1. Калькуляторы
2. Вычисления в столбик
3. Деление столбиком

Деление столбиком

ОПИСАНИЕ

Калькулятор деление столбиком онлайн поможет Вам быстро и правильно поделить натуральные числа. Калькулятор поделит число как нацело, так и выполнит деление с остатком. Кроме того, результаты деления будут проверены умножением.

РУКОВОДСТВО

Введите в соответствующие поля натуральные числа и нажмите кнопку "Рассчитать"

ТЕОРИЯ

ДЕЛЕНИЕ

Действие деление определяют с помощью действия умножения. Например, разделить число 54 на 18 - значит найти такое число, которое при умножении на 18 дает число 54. Имеем: 18 * 3 = 54, поэтому 54 : 18 = 3.

Вообще, для натуральных чисел a, b и c равенство a : b = c верно, если верно равенство b * c = a.

Рассмотрим еще несколько примеров:

156 : 12 = 13, так как 12 * 13 = 156;

345 : 15 = 23, так как 15 * 23 = 345.

В равенство a : b = c число a называют делимым, число b - делителем, число c и запись a : b - частным.

Частное a : b показывает, во сколько раз число a больше числа b или во сколько раз число b меньше числа a.

Можно ли например, вычислить частное 12 : 0? Если предположить, что такое частное существует и равно некоторому числу c, то должно выполнять равенство 0 * c = 12, но на самом деле 0 * c = 0. Следовательно, вычислить частное 12 : 0 нельзя.

А можно ли вычислить частное 0 : 0? Пусть 0 : 0 = c. Тогда 0 * c = 0. Такое равенство справедливо при любом c. А это означает, что значением числового выражения 0 : 0 может быть любое число, то есть такое частное вычислить нельзя.

Вывод: на нуль делить нельзя.

Вместе с тем, поскольку a * 0 = 0, то для любого натурального числа a верно равенство:

0 : a = 0

Также для любого натурального числа a верны равенства:

a : a = 1

a : 1 = a

Эти равенства легко проверить с помощью умножения.

АЛГОРИТМ ДЕЛЕНИЯ СТОЛБИКОМ

Рассмотрим алгоритм деления столбиком на примере:

18231 : 3, где:

18231 - делимое;

3 - делитель.

1. Запишем делимое и делитель с помощью уголка следующим образом:

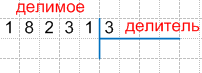
2. Определим первое неполное делимое. Для этого будем сравнивать слева направо цифры делимого с делителем, до тех пор, пока неполное делимое не станет больше делителя.

Первая цифра слева у делимого это 1. Сравним ее с делителем:

1 < 3 - цифра делимого меньше делителя, поэтому 1 не может быть первым неполным делимым. В этом случае добавим к первой цифре делимого следующую за ней, получим 18. Сравним ее с делителем:

18 > 3 - значит 18 - первое неполное делимое.

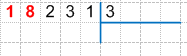
3. Разделим первое неполное делимое на делитель:

18 : 3 = 6 (остаток 0), запишем найденное частное 6 под делителем (под линией), получим:

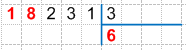
4. Проверяем деление умножением, для этого умножаем найденную цифру частного на делитель:

6 * 3 = 18, записываем произведение под первым неполным делимым и находим их разность, получаем:

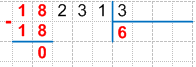
5. Сравниваем разность с делителем:

0 < 3, значит, деление первого неполного делимого мы выполнили правильно и первая цифра частного верна. Важно! Если бы разность оказалась больше делимого, то это бы означало, что первое неполное делимое мы поделили неверно.

6. Определим второе неполное делимое. Для этого снесем следующую, нами не использованную цифру делимого, вниз к найденной разности, получим:

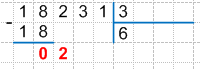
Сравним полученное число с делителем:

2 < 3, значит 2, не может быть неполным делимым. Снесем вниз следующую цифру, но при этом запишем в частное 0, так как мы сносим уже вторую цифру. Важно! Если при нахождении неполного делимого мы сносим вниз более одной цифры, то при сносе каждой цифры после первой в частное необходимо записать 0. Получаем:

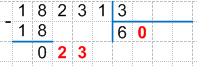
Сравним полученное число с делителем:

23 > 3, значит 23 - второе неполное делимое.

7. Разделим второе неполное делимое на делитель:

23 : 3 = 7 (остаток 2), запишем найденное неполное частное 7 под делителем (под линией), получим:

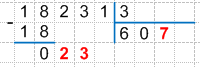
8. Проверяем деление умножением, для этого умножаем найденную цифру частного на делитель:

7 * 3 = 21, записываем произведение под вторым неполным делимым и находим их разность, получаем:

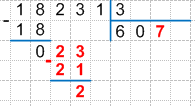
9. Сравниваем разность с делителем:

2 < 3, значит, деление второго неполного делимого мы выполнили правильно и первая цифра частного верна. Важно! Если бы разность оказалась больше делимого, то это бы означало, что второе неполное делимое мы поделили неверно.

10. Определим третье неполное делимое. Для этого снесем следующую, нами не использованную цифру делимого, вниз к найденной разности, получим:

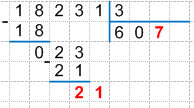
Сравним полученное число с делителем:

21 > 3, значит 21 - третье неполное делимое.

11. Разделим третье неполное делимое на делитель:

21 : 3 = 7 (остаток 0), запишем найденное частное 7 под делителем (под линией), получим:

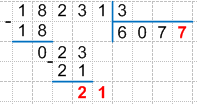
12. Проверяем деление умножением, для этого умножаем найденную цифру частного на делитель:

7 * 3 = 21, записываем произведение под третьим неполным делимым и находим их разность, получаем:

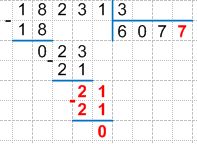
13. Сравниваем разность с делителем:

0 < 3, значит, деление третьего неполного делимого мы выполнили правильно и первая цифра частного верна. Важно! Если бы разность оказалась больше делимого, то это бы означало, что третье неполное делимое мы поделили неверно.

14. Так как, мы использовали все цифры делимого (сносить вниз больше нечего), значит деление завершено. Получаем:

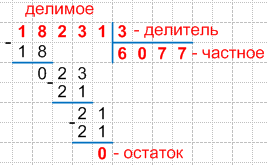
Таким образом, итоговый результат будет выглядеть следующим образом:

18231 : 3 = 6077

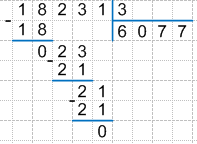
Мы рассмотрели пример деления столбиком на однозначное число. Аналогично выполняется деление на многозначное число.

Проверка деления

Проверить деление можно следующими способами:

1) Умножением, для этого необходимо частное умножить на делитель. Если в результате получится делимое, значит, деление было выполнено верно.

6077 * 3 = 18231

2) Делением, для этого необходимо делимое разделить на частное. Если в результате получится делитель, значит, деление было выполнено верно.

18231 : 6077 = 3

ДЕЛЕНИЕ С ОСТАТКОМ

Как разделить число 20 на число 6? Ответ на этот вопрос можно получить, решив следующую задачу. Как разделить поровну 20 конфет между шестерыми друзьями?

Скорее всего, каждому достанется по 3 конфеты, но при этом 2 конфеты останутся.

Такое распределение конфет иллюстрирует следующее равенство:

20 = 6 * 3 + 2.

Заметим, что 3 - это наибольшее число, произведение которого на делитель 6 меньше делимого 20. В записи 20 = 6 * 3 + 2 число 3 называют неполным частным, а число 2 - остатком. Также говорят, что при делении числа 20 на число 6 получили неполное частное, равное 3, и остаток - 2. Заметит, что остаток 2 меньше делителя 6.

Конфеты можно было разделить и другим способом, например, дать каждому по 2 конфеты и оставить 8. Ведь 20 = 6 * 2 + 8. Но здесь число 2 не является неполным частным, а число 8 - остатком.

Остаток всегда меньше делителя.

Разделим число 189 на число 13:

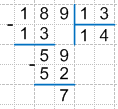
Поскольку 7 < 13, то мы вынуждены прекратить процесс деления. Это означает, что при делении числа 189 на число 13 получили неполное частное, равное 14, и остаток - 7. Имеем: 189 = 13 * 14 + 7.

Этот пример иллюстрирует такое правило.

Чтобы найти делимое, надо делитель умножить на неполное частное и прибавить остаток.

В буквенном виде это правило записывают так:

a = bq + r, где:

a - делимое, 

b - делитель,

q - неполное частное,

r - остаток, r < b.

Рассмотрим равенство 21 = 7 * 3. Его можно переписать так: 21 = 7 * 3 + 0. Говорят, что при делении числа 21 на число 7 остаток равен нулю. Также можно сказать, что число 21 делится нацело на число 7.

Проверка деления с остатком:

Чтобы проверить деление с остатком, нужно неполное частное умножить на делитель и к произведению прибавить остаток. Если в результате получится делимое, значит, деление с остатком было выполнено верно.

13 * 14 + 7 = 182 + 7 = 189