Умножение столбиком. Калькулятор
1)
2)
ОПИСАНИЕ
Калькулятор умножение столбиком онлайн поможет Вам быстро и правильно умножить натуральные числа. Результаты умножения будут проверены делением.
РУКОВОДСТВО
Введите в соответствующие поля натуральные числа и нажмите кнопку "Рассчитать"
ТЕОРИЯ
УМНОЖЕНИЕ. ПЕРЕМЕСТИТЕЛЬНОЕ СВОЙСТВО УМНОЖЕНИЯ
Начертим на листке в клетку прямоугольник со сторонами 5 см и 3 см. Разобьем его на квадраты со стороной 1 см. Как подсчитать количество этих квадратов?

Можно, например, рассуждать так. Прямоугольник разделен на три ряда, в каждом из которых есть пять квадратов. Поэтому искомое число равно 5 + 5 + 5 = 15. В левой части записанного равенства стоит сумма равных слагаемых. Как вы знаете, такую сумму записывают с помощью произведения 5 * 3. Имеем: 5 * 3 = 15.
В равенство a * b = c числа a и b называют множителями, а число c и запись a * b - произведением.
Итак, 5 * 3 = 5 + 5 + 5.
Аналогично:
3 * 5 = 3 + 3 + 3 + 3 + 3;
7 * 4 = 7 + 7 + 7 + 7;
1 * 6 = 1 + 1 + 1 + 1 + 1 + 1;
0 * 5 = 0 + 0 + 0 + 0 + 0.
В буквенном виде записывают так:
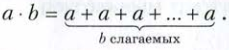
Произведением числа a на натуральное число b, не равное 1, называют сумму, состоящую из b слагаемых, каждое из которых равно a.
A если b = 1? Тогда придется рассматривать сумму, состоящую из одного слагаемого. А это в математике не принято. Поэтому договорились, что
a * 1 = a.
Если b = 0, то договорились считать, что
a * 0 = 0.
В частности,
0 * 0 = 0.
Рассмотрим произведения 1 * a и 0 * a, где a - натуральное число, отличное от 1.
Имеем:
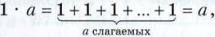
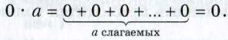
Теперь можно сделать следующие выводы.
Если один из двух множителей равен 1, то произведение равно другому множителю:
a * 1 = 1 * a = a
Если один из множителей равен нулю, то произведение равно нулю:
a * 0 = 0 * a = 0
Произведение двух чисел, отличных от нуля, нулем быть не может.
Если произведение равно нулю, то хотя бы один из множителей равен нулю.
Количество квадратов на рисунке мы подсчитали так:
5 + 5 + 5 = 5 * 3 = 15. Однако этот подсчет можно было сделать и другим способом. Прямоугольник разделен на пять столбцов, в каждом из которых есть три квадрата. поэтому искомое число квадратов равно
3 + 3 + 3 + 3 + 3 = 3 * 5 = 15.
Подсчет квадратов на рисунке двумя способами иллюстрирует переместительное свойство умножения.
Это свойство в буквенном виде записывают так:
ab = ba
АЛГОРИТМ УМНОЖЕНИЯ СТОЛБИКОМ
Умножение на однозначное число
Рассмотрим алгоритм умножения на однозначное число на примере:
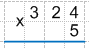
324 * 5
1. Запишем множители друг под другом, выравнивая их по правому краю, и проведем под записью черту. Важно! Большее число необходимо записать сверху, а меньшее снизу.
Получаем:
2. Начинаем поэтапно умножать числа верхнего множителя на нижний множитель, начиная с правого края. То есть сначала мы будем перемножать единицы, затем десятки, сотни и т.д.:
4 * 5 = 20, так как в результате получилось двузначное число, то под чертой, начиная с правого края, мы записываем только правую цифру двузначного числа, а левую запоминаем и прибавим ее к результату следующего произведения.
Получаем:
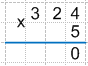
Продолжаем умножение:
2 * 5 = 10 + 2 (цифра, которую мы запомнили в предыдущем умножении) = 12, следовательно, 2 записываем в результат, а 1 запоминаем.
Получаем:
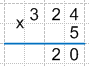
3 * 5 = 15 + 1 (цифра, которую мы запомнили в предыдущем умножении) = 16, так как мы перемножили последнюю цифру верхнего множителя, то весь результат 16 записываем под чертой.
Получаем:
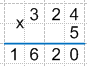
Таким образом, 324 * 5 = 1620
Умножение на двузначное число
Рассмотрим алгоритм умножения на двузначное число на примере:
324 * 25
1. Запишем множители друг под другом, выравнивая их по правому краю, и проведем под записью черту. Важно! Большее число необходимо записать сверху, а меньшее снизу.
Получаем:
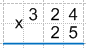
2. Перемножим поэтапно, начиная с правого края, сначала цифры верхнего множителя на цифру единиц нижнего множителя. То есть перемножим цифры верхнего множителя на 5.
4 * 5 = 20, так как в результате получилось двузначное число, то под чертой, начиная с правого края, мы записываем только правую цифру двузначного числа, а левую запоминаем и прибавим ее к результату следующего произведения.
Получаем:
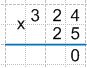
Продолжаем умножение:
2 * 5 = 10 + 2 (цифра, которую мы запомнили в предыдущем умножении) = 12, следовательно, 2 записываем в результат, а 1 запоминаем.
Получаем:
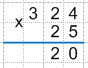
3 * 5 = 15 + 1 (цифра, которую мы запомнили в предыдущем умножении) = 16, так как мы перемножили последнюю цифру верхнего множителя, то весь результат 16 записываем под чертой.
Получаем:
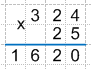
Таким образом, 324 * 5 = 1620
3. Теперь аналогично перемножим цифры верхнего множителя на цифру десятков нижнего множителя. То есть перемножим цифры верхнего множителя на 2. Однако, в этом случае, результат мы начнем записывать ниже первого произведения не с правого края, а со сдвигом на одну цифру левее. То есть при умножении на единицы запись результата начинается с единицы, при умножении на десятки - под десятками и т.д.
4 * 2 = 8 - записываем восемь в результат.
Получаем:
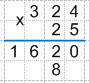
2 * 2 = 4 - записываем четыре в результат.
Получаем:
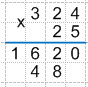
3 * 2 = 6 - записываем шесть в результат.
Получаем:
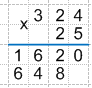
4. Теперь необходимо по правилам сложения столбиком найти сумму двух найденных произведений. Для этого ставим между произведениями знак "+", проводим ниже черту и выполняем сложение.
Получаем:
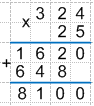
Таким образом: 324 * 25 = 8100
Аналогичным образом выполняется произведение на трехзначное, четырехзначное и т.д. число.
Умножение на число, один из разрядов которого равен нулю.
Рассмотрим алгоритм умножения на примере:
324 * 205
1. Запишем множители друг под другом, выравнивая их по правому краю, и проведем под записью черту. Важно! Большее число необходимо записать сверху, а меньшее снизу.
Получаем:
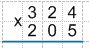
2. Перемножим поэтапно, начиная с правого края, сначала цифры верхнего множителя на цифру единиц нижнего множителя. То есть перемножим цифры верхнего множителя на 5.
Получаем:
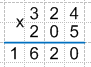
3. Теперь аналогично перемножим цифры верхнего множителя на цифру десятков нижнего множителя. То есть перемножим цифры верхнего множителя на 0. Однако, в этом случае, результат мы начнем записывать ниже первого произведения не с правого края, а со сдвигом на одну цифру левее. То есть при умножении на единицы запись результата начинается с единицы, при умножении на десятки - под десятками и т.д.
Получаем:
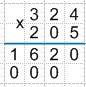
4. Теперь перемножим цифры верхнего множителя на цифру сотен нижнего множителя. То есть перемножим цифры верхнего множителя на 2. Не забываем, что результат начинаем записывать под сотнями.
Получаем:
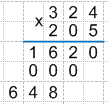
Можно заметить, что в результате умножения на 0 получились одни нули, и при нахождении суммы строка с нулями никак не будет влиять на результат. Поэтому! Если нижний множитель содержит внутри себя 0, то умножение на 0 не производится, а выполняется умножение на следующую за нулем цифру. При этом запись результата сдвигается дополнительно на одну цифру влево.
Тогда верная запись умножения будет иметь следующий вид:
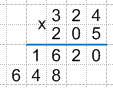
5. Теперь выполняем сложение найденных произведений и записываем итоговый результат.
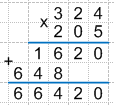
Таким образом: 324 * 205 = 66420
Умножение чисел, в конце одного из которых, либо в конце обоих стоят нули.
Рассмотрим алгоритм умножения на примере:
3240 * 2500
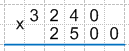
1. Главное отличие умножения таких чисел, это правило их записи столбиком. Важно! Числа, содержащие в конце себя нули, необходимо записать следующим образом:
а) Мысленно отбрасываем у данных чисел нули и записываем получившиеся числа по правилам умножения в столбик. То есть выравниваем их по правому краю, причем большее из получившихся чисел записываем сверху, а меньшее снизу.
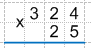
б) Дописываем отброшенные нули.
2. Перемножим 324 * 25 по правилам умножения столбиком. Важно! Стоящие справа нули в умножении не используем, то есть не обращаем на них пока внимание.
Получаем:
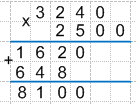
3. Теперь к получившемуся результату необходимо добавить справа те нули, которые мы не использовали при умножении. То есть добавляем 3 нуля.
Получаем:
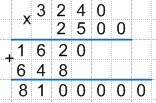
Таким образом, 3240 * 2500 = 8100000
Правильность умножения можно проверить делением. Если при делении произведения на один из множитель получится второй множитель, значит, умножение было выполнено верно.
Таким образом:
8100000 : 3240 = 2500
8100000 : 2500 = 3240
СОЧЕТАТЕЛЬНОЕ И РАСПРЕДЕЛИТЕЛЬНОЕ СВОЙСТВА УМНОЖЕНИЯ
Начертим на листке в клетку прямоугольник со сторонами 5 см и 3 см. Разобьем его на квадраты со стороной 1 см.

Подсчитаем количество клеток, расположенных в прямоугольнике. Это можно сделать, например, так.
Количество квадратов со стороной 1 см равно 5 * 3. Каждый такой квадрат состоит из четырех клеток. Поэтому общее число клеток равно (5 * 3) * 4.
Эту же задачу можно решить иначе. Каждый из пяти столбцов прямоугольника состоит из трех квадратов со стороной 1 см. Поэтому в одном столбце содержится 3 * 4 клеток. Следовательно, всего клеток будет 5 * (3 * 4).
Подсчет клеток на рисунке двумя способами иллюстрирует сочетательное свойство умножения для чисел 5, 3 и 4. Имеем: (5 * 3) * 4 = 5 * (3 * 4).
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел.
В буквенном виде это свойство записывают так:
(ab)c = a(bc)
Из переместительного и сочетательного свойств умножения следует, что при умножении нескольких чисел множители можно менять местами и заключать в скобки, тем самым определяя порядок вычислений.
Например, верны равенства:
abc = cba,
17 * 2 * 3 * 5 = (17 * 3) * (2 * 5).
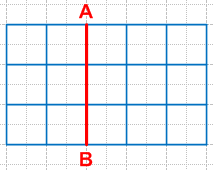
На вышеприведенном рисунке отрезок AB делит рассмотренный выше прямоугольник на прямоугольник и квадрат.
Подсчитаем количество квадратов со стороной 1 см двумя способами.
С одной стороны, в образовавшемся квадрате их содержится 3 * 3, а в прямоугольника - 3 * 2. Всего получим 3 * 3 + 3 * 2 квадратов. С другой стороны, в каждой из трех строчек данного прямоугольника находится 3 + 2 квадрата. Тогда их общее количество равно 3 * (3 + 2).
Равенство 3 * (3 + 2) = 3 * 3 + 3 * 2 иллюстрирует распределительное свойство умножения.
Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить.
В буквенном виде это свойство записывают так:
a(b + c) = ab + ac
Из распределительного свойства умножения относительно сложения следует, что
ab + ac = a(b + c).
Это равенство позволяет формулу P = 2a + 2b для нахождения периметра прямоугольника записать в таком виде:
P = 2(a + b).
Заметим, что распределительное свойство справедливо для трех и более слагаемых. Например:
a(m + n + p + q) = am + an + ap + aq.
Также справедливо распределительное свойство умножения относительно вычитания: если b > c или b = c, то
a(b - c) = ab - ac
